The following article is published in ESO Messenger (Dong, Subo et al., 2019, Msngr, 178, 45)
Accompanying Video see ESOcast 192 Light: “GRAVITY Resolves a Gravitationally Microlensed Star”

Image Credits: ESO
In 1936, after persistent prodding by the amateur scientist Rudi Mandl, Albert Einstein reluctantly published the idea of gravitational microlensing (Einstein, 1936), which was “a little calculation” he had carried out 24 years earlier. According to general relativity, when an object (i.e., a lens) aligns closely with a background star (i.e., a source) along the line of sight of the observer, the light rays from the source are bent when passing by the lens and subsequently form images. In the ideal case of perfect alignment, the bent light rays form a ring-like image (called the Einstein ring); more typically, there are two arc-shaped images with a separation on the scale of the Einstein ring. For microlensing in the Galaxy, the angular radius of the Einstein ring (the angular Einstein radius) is on the order of only a milliarcsecond.
Einstein’s reluctance to publish was because he saw little in the way of observational prospects; he asserted that “there is no hope of observing this phenomenon directly”. He had two reasons for thinking this, both of which relate to the minuscule angular size of the Einstein ring. First, for microlensing to occur, two stars need to align within the Einstein ring, and the probability of this is tiny, no greater than one in a million towards any star in the Galaxy. Second, he anticipated that no instruments could resolve the images, and thus the only observable effect would be the brightening of the source.
Since 1993, armed with wide-field telescopes and CCD cameras, time-domain surveys have vastly exceeded Einstein’s pessimistic expectation and found tens of thousands of microlensing events so far by photometrically monitoring almost a billion stars in dense stellar fields (primarily the Galactic bulge). During these events, the brightness of the source usually varies over a few weeks as the lens star moves with a relative proper motion of several milli-arcseconds per year. Microlensing events have yielded rich astrophysical results, including the discovery of nearly a hundred extrasolar planets.
It was not until November 2017 that microlensed images were successfully resolved for the first time (Dong et al., 2019), defying Einstein’s dismissal. Our team achieved this by observing the microlensing event TCP J05074264+2447555 (hereafter “TCP J0507+2447” for brevity) with the GRAVITY instrument (GRAVITY Collaboration, 2017) on the Very Large Telescope Interferometer (VLTI). Our observations allow us to measure the angular Einstein radius at 2% precision: 1.87 ± 0.03 milliarcseconds (see Figure 1). Interferometric resolution of images can unleash microlensing’s unique potential to find isolated stellar-mass black holes (BHs) lurking in the Galaxy by lifting the degeneracy between mass and distance in the analysis of microlensing light curves.
LIGO/VIRGO’s astonishing discoveries of merging BHs (Abbott et al., 2016) have raised an important open question: how to form BHs with a few tens of solar masses? Whether they are the end points of massive stars or have exotic origins in the early universe, theories predict that isolated (single) BHs must exist. The relative frequency between the single and binary BH populations can provide crucial clues to the formation mechanism. However, limited by the detection techniques, all known stellar-mass BHs are found in binaries.
Microlensing holds great promise in probing the important yet uncharted parameter space of isolated BHs. Estimates by Gould (2000) suggest that, amongst the microlensing events detected to date, many hundreds may involve BH lenses. But thus far only a few BH candidates have been reported. This is due to the mass-distance-velocity parameter degeneracy, which makes it impossible to definitively distinguish BHs from low-mass stars. All existing BH candidates have relatively long event timescales, which can be due to the large Einstein radii of BH lenses with high masses. But a large Einstein radius can also be produced by a low-mass stellar lens at a close distance. Alternatively, a slow relative proper motion between the lens and source stars may induce a long timescale even with a moderate Einstein radius.
To completely break the degeneracy, two additional observables are required besides the microlensing event timescale. One is called the “microlensing parallax”, which depends on the Einstein radius projected onto the observer’s plane. It can be constrained for long events from the distortion of the light curves induced by the acceleration of the Earth while it orbits the Sun or by comparing the ground-based observations with simultaneous light curves from a space telescope in heliocentric orbit. The angular Einstein radius measured from the VLTI resolution of microlensed images is the other missing ingredient that can yield unambiguous determination of the lens mass and thereby definitively identify a BH lens.
The lens of TCP J0507+2447 is not a BH but a low-mass star. Nevertheless, it can serve as a testbed for the above-mentioned approach of lens mass determination. In an independent effort, another research team has measured the lens flux with Keck adaptive optics images, and by combining this with our precise VLTI angular Einstein radius measurement, they find that the lens is a dwarf star of 0.58 +/- 0.03 M⊙ (Fukui et al., 2019). Our team (Zang et al., Submitted) has measured the microlens parallax using the Spitzer light curves, and by combining the VLTI angular Einstein radius, the lens is found to be 0.50 +/- 0.06 M⊙. The good agreement between the results of these two approaches demonstrates the robustness of our method. Remarkably, around the peak of the light curve of TCP J0507+2447, there was a short-lived anomaly lasting a few hours, suggesting that the lens star has a 20-Earth-mass planet at around 1 AU (Nucita et al., 2018; Fukui et al., 2019).
The possibility of using the VLTI to resolve microlensing images was first proposed by Delplancke et al. (2001), but it had proven to be extremely challenging, with numerous failed attempts prior to our observations. The major challenge had been the difficulty of identifying a sufficiently bright target for the interferometric observations. A confluence of lucky circumstances facilitated our success. Unlike the vast majority of microlensing events found by professional wide-field surveys towards the Galactic bulge, TCP J0507+2447 was serendipitously discovered by the Japanese amateur astronomer T. Kojima, and the source is at 800 pc towards the Galactic anti-centre, making it one of the closest microlensing events ever found. Our DDT proposal (2100.D-5031) was quickly accepted, and an ongoing VLTI run allowed our GRAVITY observations to be conducted within about a week of the initial discovery. And thanks to the exceptional site conditions, we were able to observe it near the magnitude limit of VLTI/GRAVITY at a relatively high airmass of ~ 1.5.
The exceptional sensitivity of VLTI/GRAVITY and the advent of all-sky bright transient surveys such as ASAS-SN and Gaia provide an unprecedented opportunity to obtain more resolved microlensing images. We hope to carry out a systematic survey towards the first definitive identification of an isolated stellar-mass black hole.
References
Abbott, B. et al. 2016, Phys. Rev. Lett., 116, 1102
Einstein, A. 1936, Science, 84, 506
Dong, S. et al. 2019, ApJ, 871, 70
Delplancke, F. et al. 2001, A&A, 375, 701
Fukui, A. et al. 2019, AJ, 158, 206
Gould, A. 2000, ApJ, 535, 928
Gravity Collaboration 2017, A&A, 602, 94
Nucita, A. et al. 2018, MNRAS, 476, 2962
Zang et al., 2019, Submitted to ApJ, (arXiv:1912.00038)
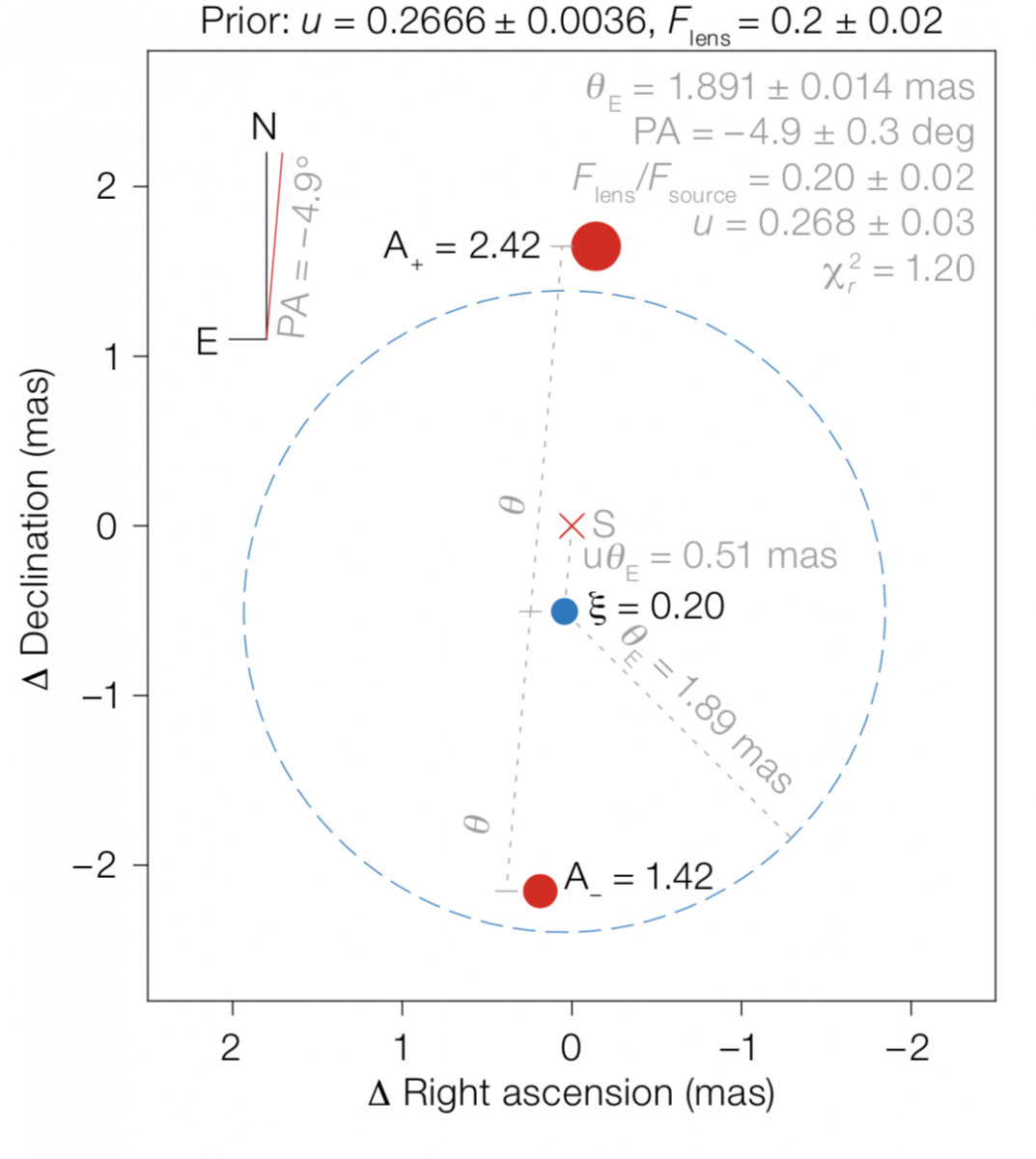
Figure 1. Model of the apparent image. The two red dots are the major and minor images — the sizes of the dots do not represent the actual apparent sizes of the images, but rather an indication of their respective fluxes. The ’x’ symbol is where the unlensed source would be (labelled “S”). The blue dot is the lens position with its flux, and the blue dashed circle is its Einstein ring. Flux is expressed in fractions of unlensed source flux.
PKU News: http://news.pku.edu.cn/jxky/1ad2f756c06344bd85ae9ecd3958d4f3.htm